「PerlinNoise で良い感じにオブジェクトを配置するネタ」の続きです。空間中に配置するオブジェクトを良い感じにグルーピングしたいことは良くあります(多分)。 グリッドベースで管理したり、総当たりで距離を判定したり、事によっては K-Means 法などを使ってクラスタリングするなどの方法があります。

先日のパッと思いついた割と運頼りで精度は高くないけど、高速かつそれっぽくグループ分けするアルゴリズムを紹介します。 もしかすると名前なんかはついてる手法(アルゴリズム)なのかもしれませんが、私には分からないです。

このサンプルでは、PerlinNoise を使って配置するオブジェクトの色を何となくグループごとに分けています。 例えば植物を配置しようとするとき、似た植物は隣接する位置に同種の植物などが群生しますから、こういった手法が生きると思います。

アルゴリズムの概要

ソースコードを見ながら追うのが良いと思います。複雑な手続き、複雑な関数・数学は利用していません。 PerlinNoiseObjectGeneratorWithColor.cs ファイルの UpdateColorDistributionData 関数がここで解説する処理を実装しています。

手法のコアな部分は下記のような分布マップ(分布データのリスト)を作ることにあります。ここではカラー情報の分布マップです。

ランダムに頂点をサンプリング(ここでは PerlinNoise に従ってサンプリング)して、その座標を新規の分布データとし、分布データのリストを更新します。

新規の分布データを加えるときに条件が付きます。 既存の分布データのリストから最寄りの分布データを検出し、新規の分布データとの距離を算出します。

(1)この距離が離れているとき、新規の分布データを新たな分布データ(グループ)として、既存の分布データのセットに追加します。 ここでは新しい色情報を持たせていますから、色データを持たせています(図の緑)。

(2) 最寄りの分布データと新規の分布データの距離が近いとき、その中間点を算出し、既存の、最寄りの分布データを更新します。 このとき色情報は最寄りの分布データのものをそのまま継承します。

これを繰り返し実行することで、分布マップが生成されます。

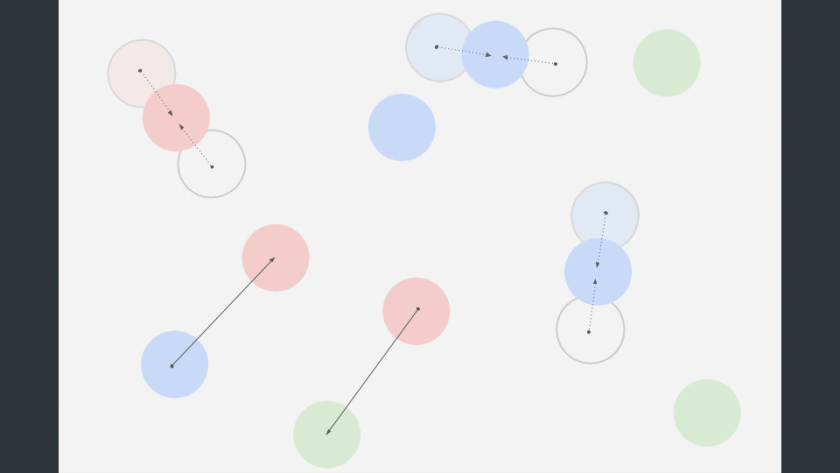
初回の起動時にあらかじめ分布マップを生成しておき、実際にオブジェクトを追加する際にも、この手順を繰り返します。

ソースコードの一部を解説

主要なアルゴリズムは先のもので全てで、、ソースコードはそのまま実装されています。 拙い解説の足しにソースコードを読んでいただければ概ねどのような処理を実行しているのか理解していただけると思います。

分布データを示す構造体 ColorDistributionData を定義している点に注意してください。 もしグループにまとめられたオブジェクトを一括して参照したい場合などには、List などをフィールドに持つ、class を定義する必要があります。 シチュエーションに応じて実装方法を変更してください。

protected struct ColorDistributionData
{
	public Color   color;
	public Vector3 position;
}

public Color[] objectColors;
public int     distributionSeedCount = 8;
public float   nearDistributionThreshold = 10;

protected List<ColorDistributionData> colorDistributionDataList
    = new List<ColorDistributionData>();

…

float minlength = Vector3.SqrMagnitude
                 (position - this.colorDistributionDataList[0].position);
int   minlengthindex = 0;

// (1) 既存の分布データの中から近い距離にある分布データを探します。

for (int i = 1; i < this.colorDistributionDataList.Count; i++)
{
	float length = Vector3.SqrMagnitude
                       (position - this.colorDistributionDataList[i].position);

	if (length < minlength)
	{
		minlength = length;
		minlengthindex = i;
	}
}

// (2) 既存の最寄りの分布データと距離が離れていたら新しい分布データとして採用します。

ColorDistributionData minLengthColorDistributionData
    = this.colorDistributionDataList[minlengthindex];

Color objectColor;

if (this.nearDistributionThreshold < minlength)
{
	objectColor = this.objectColors[Random.Range(0, this.objectColors.Length)];

	this.colorDistributionDataList.Add(new ColorDistributionData()
	{
		color = objectColor,
		position = position
	});
}

// (3) 既存の分布データと距離が近ければ中間の位置を分布データとして書き換えます。

else
{
	objectColor = minLengthColorDistributionData.color;

	this.colorDistributionDataList[minlengthindex] = new ColorDistributionData()
	{
		color = objectColor,
		position = (minLengthColorDistributionData.position + position) / 2,
	};
}

return objectColor;

このアルゴリズムの利点と欠点

このアルゴリズムの利点は高速に動作し、それっぽい結果が得られることです。 一方で精度が高くないところは欠点です。乱数で分布を更新している場合は特に、サンプリングの順序で得られる結果が変わります。 分布データの中心点が、常に移動(変化)するためです。

今回の例で言えば、二つの分布データのちょうど中間あたりにオブジェクトが配置されるときなどに、 2 色以上が混ざりあった結果が得られます。

ただし、オブジェクトが配置される場所、サンプリングされる位置が十分に離れるようなパラメータ設定のときは、精度が上がります。

また、今回の例で言えば、左上から順に右下に向かってオブジェクトの生成を実行する、などすれば、精度は上がります。 ただし、現実的にそのような使い方は少ないと思います。

テクスチャやステージなどのリソースを作る様なシチュエーションならあり得るかもしれません。しかしそれであればより高精度の手法を使った方が良いような気はします。